题目描述
在数轴上有 n 个闭区间 [l1,r1],[l2,r2],...,[ln,rn]。现在要从中选出 m 个区间,使得这 m 个区间共同包含至少一个位置。换句话说,就是使得存在一个 x,使得对于每一个被选中的区间 [li,ri],都有 li≤x≤ri。
对于一个合法的选取方案,它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 [li,ri] 的长度定义为 ri−li,即等于它的右端点的值减去左端点的值。
求所有合法方案中最小的花费。如果不存在合法的方案,输出 −1。
输入格式
第一行包含两个正整数 n,m 用空格隔开,意义如上文所述。保证 1≤m≤n。
接下来 n 行,每行表示一个区间,包含用空格隔开的两个整数 li 和 ri 为该区间的左右端点。
输出格式
只有一行,包含一个正整数,即最小花费。
样例
6 3
3 5
1 2
3 4
2 2
1 5
1 4
2
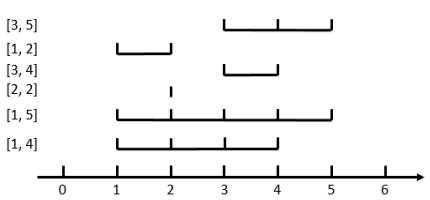
如图,当 n=6,m=3 时,花费最小的方案是选取 [3,5]、[3,4]、[1,4] 这三个区间,他们共同包含了 4 这个位置,所以是合法的。其中最长的区间是 [1,4],最短的区间是 [3,4],所以它的花费是 (4−1)−(4−3)=2。
数据范围与提示
所有测试数据的范围和特点如下表所示:
| 测试点编号 |
n |
m |
li,ri |
| 1 |
20 |
9 |
0≤li≤ri≤100 |
| 2 |
10 |
| 3 |
199 |
3 |
0≤li≤ri≤100000 |
| 4 |
200 |
| 5 |
1000 |
2 |
| 6 |
2000 |
| 7 |
199 |
60 |
0≤li≤ri≤5000 |
| 8 |
200 |
50 |
| 9 |
0≤li≤ri≤109 |
| 10 |
1999 |
500 |
0≤li≤ri≤5000 |
| 11 |
2000 |
400 |
| 12 |
500 |
0≤li≤ri≤109 |
| 13 |
30000 |
2000 |
0≤li≤ri≤100000 |
| 14 |
40000 |
1000 |
| 15 |
50000 |
15000 |
| 16 |
100000 |
20000 |
| 17 |
200000 |
0≤li≤ri≤109 |
| 18 |
300000 |
50000 |
| 19 |
400000 |
90000 |
| 20 |
500000 |
200000 |

