肖飞老师的哲学之道
该比赛已结束,您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。
题目描述
肖飞老师在编程之余,酷爱哲学。树林有助于肖老师对哲学的思考,但它们像迷宫一样密密麻麻地栽种着。肖老师的步道是在一条有许多树林的方形区域的小路,由于肖老师思考得极其投入,以致于在树林中散步时经常迷失了方向。
幸运的是,虽然肖老师每次前往的树林不一样,但树林的步道结构都是相似的:按同样的规则在的正方形土地上设计和构建。设计路径的规则是:当时,每走一米后右转90°,当时,行走路线由前一种行走路线的不同形式组成。下图显示了肖老师的三次行走路线,分别是的情况。对于的情况,肖老师的行走路线由四个结构组成,左下和右下的结构分别是上一个行走路线顺时针和逆时针旋转90°得到,左上和右上的结构则与上一个行走路线相同,然后将这四个结构连接起来,就构成了肖老师的行走路线。这种行走的规则是由数学哲学家David Hilbert设计的,由此产生的路径通常被称为希尔伯特曲线。他曾经讲过一种空间填充方法,用这种曲线来填充满一个平面正方形,肖老师的行走路线都是按照这种方法设计的。
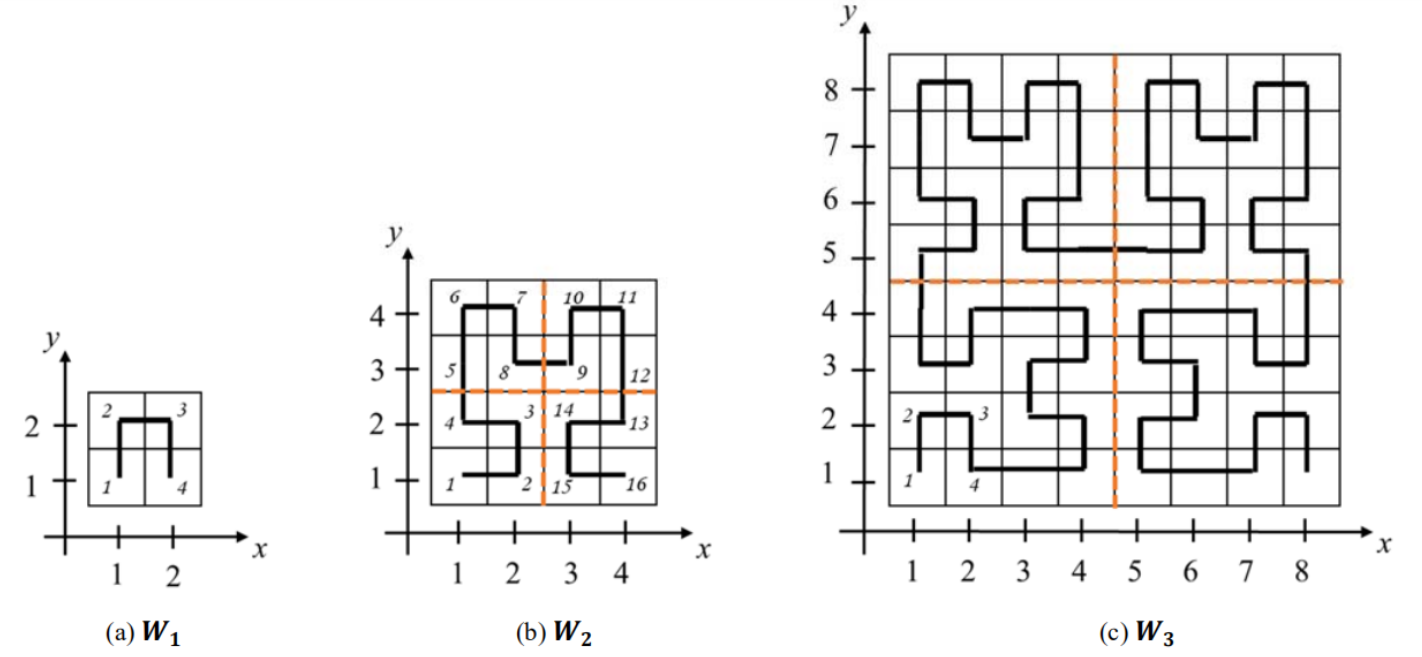
由于树林所处的环境因素,计算机学院的ACM团队将使用热气球营救在树林里迷路的肖老师。肖老师每次在树林里思考问题时,都会记下自己走了多少步,ACM团队也知道肖老师所在树林的边长。因为位置偏僻,定位系统无法使用,所以ACM团队必须确定肖老师所在的位置,即坐标。假设肖老师的步道位于平面直角坐标系,左下角块的坐标为。肖老师的入口总是在,出口总是在,为正方形的边长。同时,假设肖老师在入口处已经走了一米的道路,他只会向前走,不会后退。例如,在b图中,肖老师走了10步,因此他的坐标为
你的任务是写一个程序来帮助ACM团队,根据肖老师走了几米的路和他所在的树林的边长,使用你写的程序来报告肖老师目前所在的目标。快点!肖飞老师急需你的帮助。
输入格式
仅一行,输入两个整数和,并用空格分隔。表示肖老师所在树林的边长,表示肖老师所走的距离是多少米。数据范围分别是是,,。
输出格式
仅一行,输出肖老师所在的坐标和,以空格分隔。
样例
4 13
4 2
8 19
2 6
HGNU ACM Training Round #13
- 状态
- 已结束
- 规则
- ACM/ICPC
- 题目
- 12
- 开始于
- 2024-7-24 13:00
- 结束于
- 2024-7-24 18:00
- 持续时间
- 5 小时
- 主持人
- 参赛人数
- 15
